Pipeline for phase change materials. Scripting example

Consists of three sections:

Separate sample from background
Crystallinity map generation
Region clustering

File: 4D STEM of phase change material, Vadim Migunov et al. TODO update to proper credit

[1]:

%matplotlib inline

import functools
import os

from skimage.feature import peak_local_max
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
import sklearn.feature_extraction
import sklearn.cluster
import scipy.sparse
import sparse

from libertem.udf import UDF
from libertem import masks
from libertem.api import Context
from libertem.udf.masks import ApplyMasksUDF
from libertem.udf.stddev import run_stddev
from  libertem.udf.crystallinity import run_analysis_crystall

Crystallinity map generation

[2]:

data_base_path = os.environ.get("TESTDATA_BASE_PATH", "/home/alex/Data/")

[3]:

ctx = Context()
ds = ctx.load("auto", path=os.path.join(data_base_path, "01_ms1_3p3gK.hdr"))

/home/weber/miniconda3/envs/libertem39/lib/python3.9/site-packages/distributed/node.py:182: UserWarning: Port 8787 is already in use.
Perhaps you already have a cluster running?
Hosting the HTTP server on port 42581 instead
  warnings.warn(
2023-01-12 17:50:10,530 - distributed.diskutils - INFO - Found stale lock file and directory '/tmp/dask-worker-space-20335/worker-oe_35td4', purging
2023-01-12 17:50:10,531 - distributed.diskutils - INFO - Found stale lock file and directory '/tmp/dask-worker-space-20335/worker-50ef5ulu', purging
2023-01-12 17:50:10,532 - distributed.diskutils - INFO - Found stale lock file and directory '/tmp/dask-worker-space-20335/worker-ck95u0t2', purging
2023-01-12 17:50:10,532 - distributed.diskutils - INFO - Found stale lock file and directory '/tmp/dask-worker-space-20335/worker-lybxcia2', purging
2023-01-12 17:50:10,532 - distributed.diskutils - INFO - Found stale lock file and directory '/tmp/dask-worker-space-20335/worker-93dcpf3n', purging
2023-01-12 17:50:10,532 - distributed.diskutils - INFO - Found stale lock file and directory '/tmp/dask-worker-space-20335/worker-het0djnp', purging
2023-01-12 17:50:10,533 - distributed.diskutils - INFO - Found stale lock file and directory '/tmp/dask-worker-space-20335/worker-m985abxl', purging
2023-01-12 17:50:10,533 - distributed.diskutils - INFO - Found stale lock file and directory '/tmp/dask-worker-space-20335/worker-2v96oug_', purging
2023-01-12 17:50:10,533 - distributed.diskutils - INFO - Found stale lock file and directory '/tmp/dask-worker-space-20335/worker-bnwmn08s', purging
2023-01-12 17:50:10,533 - distributed.diskutils - INFO - Found stale lock file and directory '/tmp/dask-worker-space-20335/worker-ygtzyb6x', purging
2023-01-12 17:50:10,533 - distributed.diskutils - INFO - Found stale lock file and directory '/tmp/dask-worker-space-20335/worker-6zeb__8s', purging
2023-01-12 17:50:10,534 - distributed.diskutils - INFO - Found stale lock file and directory '/tmp/dask-worker-space-20335/worker-tnnf3nho', purging
2023-01-12 17:50:10,534 - distributed.diskutils - INFO - Found stale lock file and directory '/tmp/dask-worker-space-20335/worker-gdpqscj5', purging
2023-01-12 17:50:10,534 - distributed.diskutils - INFO - Found stale lock file and directory '/tmp/dask-worker-space-20335/worker-sajso3og', purging
2023-01-12 17:50:10,534 - distributed.diskutils - INFO - Found stale lock file and directory '/tmp/dask-worker-space-20335/worker-y84m7dww', purging
2023-01-12 17:50:10,535 - distributed.diskutils - INFO - Found stale lock file and directory '/tmp/dask-worker-space-20335/worker-5qjjm5e5', purging
2023-01-12 17:50:10,535 - distributed.diskutils - INFO - Found stale lock file and directory '/tmp/dask-worker-space-20335/worker-h1jmfhw4', purging
2023-01-12 17:50:10,535 - distributed.diskutils - INFO - Found stale lock file and directory '/tmp/dask-worker-space-20335/worker-1ncnrkmo', purging
2023-01-12 17:50:10,535 - distributed.diskutils - INFO - Found stale lock file and directory '/tmp/dask-worker-space-20335/worker-vq2sj4lm', purging
2023-01-12 17:50:10,536 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=13)
2023-01-12 17:50:10,536 - distributed.utils - INFO - Reload module tmpedemyzkf from .py file
2023-01-12 17:50:10,547 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=3)
2023-01-12 17:50:10,547 - distributed.utils - INFO - Reload module tmpo8pp_z_5 from .py file
2023-01-12 17:50:10,563 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=8)
2023-01-12 17:50:10,564 - distributed.utils - INFO - Reload module tmp5mluv688 from .py file
2023-01-12 17:50:10,578 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CUDA", device=0)
2023-01-12 17:50:10,578 - distributed.utils - INFO - Reload module tmpnxq79s_0 from .py file
2023-01-12 17:50:10,589 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=0)
2023-01-12 17:50:10,590 - distributed.utils - INFO - Reload module tmpx5pmp97x from .py file
2023-01-12 17:50:10,604 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=20)
2023-01-12 17:50:10,605 - distributed.utils - INFO - Reload module tmpm9h4px9q from .py file
2023-01-12 17:50:10,631 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=21)
2023-01-12 17:50:10,632 - distributed.utils - INFO - Reload module tmpmpk0g3ya from .py file
2023-01-12 17:50:10,664 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=11)
2023-01-12 17:50:10,664 - distributed.utils - INFO - Reload module tmphk8i5ih8 from .py file
2023-01-12 17:50:10,677 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=1)
2023-01-12 17:50:10,677 - distributed.utils - INFO - Reload module tmputytzkdn from .py file
2023-01-12 17:50:10,696 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=10)
2023-01-12 17:50:10,697 - distributed.utils - INFO - Reload module tmp0tjfg2l9 from .py file
2023-01-12 17:50:10,703 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=7)
2023-01-12 17:50:10,703 - distributed.utils - INFO - Reload module tmpd_g_silm from .py file
2023-01-12 17:50:10,714 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=18)
2023-01-12 17:50:10,715 - distributed.utils - INFO - Reload module tmpjgmht48i from .py file
2023-01-12 17:50:10,733 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=14)
2023-01-12 17:50:10,733 - distributed.utils - INFO - Reload module tmp60t2lwfv from .py file
2023-01-12 17:50:10,742 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=15)
2023-01-12 17:50:10,743 - distributed.utils - INFO - Reload module tmpfa84m_xz from .py file
2023-01-12 17:50:10,768 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=4)
2023-01-12 17:50:10,768 - distributed.utils - INFO - Reload module tmp2q39qek3 from .py file
2023-01-12 17:50:10,775 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=2)
2023-01-12 17:50:10,775 - distributed.utils - INFO - Reload module tmpj6m3i3ov from .py file
2023-01-12 17:50:10,790 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=5)
2023-01-12 17:50:10,790 - distributed.utils - INFO - Reload module tmpkf_qnoew from .py file
2023-01-12 17:50:10,812 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=22)
2023-01-12 17:50:10,813 - distributed.utils - INFO - Reload module tmpzgtfrjqg from .py file
2023-01-12 17:50:10,838 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=6)
2023-01-12 17:50:10,838 - distributed.utils - INFO - Reload module tmpxii_na8e from .py file
2023-01-12 17:50:10,841 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=16)
2023-01-12 17:50:10,841 - distributed.utils - INFO - Reload module tmpdpfrnuvy from .py file
2023-01-12 17:50:10,869 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=19)
2023-01-12 17:50:10,870 - distributed.utils - INFO - Reload module tmpt5zrb1f7 from .py file
2023-01-12 17:50:10,872 - distributed.preloading - INFO - Import preload module: /tmp/tmpedemyzkf.py
2023-01-12 17:50:10,873 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-13', service_id='13')
2023-01-12 17:50:10,873 - distributed.utils - INFO - Reload module tmpte9dt25z from .py file
2023-01-12 17:50:10,873 - distributed.preloading - INFO - Import preload module: /tmp/tmpte9dt25z.py
2023-01-12 17:50:10,873 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:10,877 - distributed.preloading - INFO - Import preload module: /tmp/tmpo8pp_z_5.py
2023-01-12 17:50:10,877 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-3', service_id='3')
2023-01-12 17:50:10,878 - distributed.utils - INFO - Reload module tmp3dp_a05z from .py file
2023-01-12 17:50:10,878 - distributed.preloading - INFO - Import preload module: /tmp/tmp3dp_a05z.py
2023-01-12 17:50:10,878 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:10,886 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=12)
2023-01-12 17:50:10,887 - distributed.utils - INFO - Reload module tmpnknaw25k from .py file
2023-01-12 17:50:10,900 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=9)
2023-01-12 17:50:10,900 - distributed.utils - INFO - Reload module tmpkg1evcn9 from .py file
2023-01-12 17:50:10,907 - distributed.preloading - INFO - Import preload module: /tmp/tmpnxq79s_0.py
2023-01-12 17:50:10,907 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cuda-0', service_id='0')
2023-01-12 17:50:10,908 - distributed.utils - INFO - Reload module tmpkouq_r69 from .py file
2023-01-12 17:50:10,908 - distributed.preloading - INFO - Import preload module: /tmp/tmpkouq_r69.py
2023-01-12 17:50:10,908 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:10,912 - distributed.preloading - INFO - Import preload module: /tmp/tmpm9h4px9q.py
2023-01-12 17:50:10,912 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-20', service_id='20')
2023-01-12 17:50:10,913 - distributed.utils - INFO - Reload module tmpkwit4q49 from .py file
2023-01-12 17:50:10,913 - distributed.preloading - INFO - Import preload module: /tmp/tmpkwit4q49.py
2023-01-12 17:50:10,913 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:10,920 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:10,925 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:10,938 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=23)
2023-01-12 17:50:10,938 - distributed.preloading - INFO - Import preload module: /tmp/tmpmpk0g3ya.py
2023-01-12 17:50:10,939 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-21', service_id='21')
2023-01-12 17:50:10,939 - distributed.utils - INFO - Reload module tmpblrzbrp4 from .py file
2023-01-12 17:50:10,939 - distributed.utils - INFO - Reload module tmpeak_jesu from .py file
2023-01-12 17:50:10,939 - distributed.preloading - INFO - Import preload module: /tmp/tmpeak_jesu.py
2023-01-12 17:50:10,939 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:10,955 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:10,964 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:10,989 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:10,999 - distributed.preloading - INFO - Import preload module: /tmp/tmphk8i5ih8.py
2023-01-12 17:50:10,999 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-11', service_id='11')
2023-01-12 17:50:10,999 - distributed.utils - INFO - Reload module tmpcjrxaf00 from .py file
2023-01-12 17:50:11,000 - distributed.preloading - INFO - Import preload module: /tmp/tmpcjrxaf00.py
2023-01-12 17:50:11,000 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:11,005 - distributed.preloading - INFO - Import preload module: /tmp/tmp5mluv688.py
2023-01-12 17:50:11,006 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-8', service_id='8')
2023-01-12 17:50:11,006 - distributed.utils - INFO - Reload module tmpnz3vlscu from .py file
2023-01-12 17:50:11,006 - distributed.preloading - INFO - Import preload module: /tmp/tmpnz3vlscu.py
2023-01-12 17:50:11,007 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:11,011 - distributed.preloading - INFO - Import preload module: /tmp/tmpd_g_silm.py
2023-01-12 17:50:11,011 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-7', service_id='7')
2023-01-12 17:50:11,011 - distributed.utils - INFO - Reload module tmptimw3stx from .py file
2023-01-12 17:50:11,012 - distributed.preloading - INFO - Import preload module: /tmp/tmptimw3stx.py
2023-01-12 17:50:11,012 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:11,012 - distributed.preloading - INFO - Import preload module: /tmp/tmputytzkdn.py
2023-01-12 17:50:11,012 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-1', service_id='1')
2023-01-12 17:50:11,013 - distributed.utils - INFO - Reload module tmp9g6vby4f from .py file
2023-01-12 17:50:11,013 - distributed.preloading - INFO - Import preload module: /tmp/tmp9g6vby4f.py
2023-01-12 17:50:11,013 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:11,017 - distributed.preloading - INFO - Import preload module: /tmp/tmpx5pmp97x.py
2023-01-12 17:50:11,017 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-0', service_id='0')
2023-01-12 17:50:11,018 - distributed.utils - INFO - Reload module tmpwzhjguen from .py file
2023-01-12 17:50:11,018 - distributed.preloading - INFO - Import preload module: /tmp/tmpwzhjguen.py
2023-01-12 17:50:11,018 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:11,023 - distributed.preloading - INFO - Import preload module: /tmp/tmp0tjfg2l9.py
2023-01-12 17:50:11,023 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-10', service_id='10')
2023-01-12 17:50:11,023 - distributed.utils - INFO - Reload module tmpstgvlaee from .py file
2023-01-12 17:50:11,023 - distributed.preloading - INFO - Import preload module: /tmp/tmpstgvlaee.py
2023-01-12 17:50:11,024 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:11,025 - distributed.preloading - INFO - Creating preload: from libertem.executor.dask import worker_setup; worker_setup(resource="CPU", device=17)
2023-01-12 17:50:11,026 - distributed.utils - INFO - Reload module tmpl3_x3umv from .py file
2023-01-12 17:50:11,043 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-service-0', service_id='0')
2023-01-12 17:50:11,043 - distributed.utils - INFO - Reload module tmpc7avhpah from .py file
2023-01-12 17:50:11,046 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:11,056 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:11,060 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:11,061 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:11,066 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:11,070 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:11,074 - distributed.preloading - INFO - Import preload module: /tmp/tmpfa84m_xz.py
2023-01-12 17:50:11,074 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-15', service_id='15')
2023-01-12 17:50:11,074 - distributed.utils - INFO - Reload module tmpcxcjn6ec from .py file
2023-01-12 17:50:11,075 - distributed.preloading - INFO - Import preload module: /tmp/tmpcxcjn6ec.py
2023-01-12 17:50:11,075 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:11,085 - distributed.preloading - INFO - Import preload module: /tmp/tmp2q39qek3.py
2023-01-12 17:50:11,085 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-4', service_id='4')
2023-01-12 17:50:11,085 - distributed.utils - INFO - Reload module tmpqug677m3 from .py file
2023-01-12 17:50:11,086 - distributed.preloading - INFO - Import preload module: /tmp/tmpqug677m3.py
2023-01-12 17:50:11,086 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:11,127 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:11,128 - distributed.preloading - INFO - Import preload module: /tmp/tmpkf_qnoew.py
2023-01-12 17:50:11,129 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-5', service_id='5')
2023-01-12 17:50:11,129 - distributed.utils - INFO - Reload module tmpiatdzhbv from .py file
2023-01-12 17:50:11,130 - distributed.preloading - INFO - Import preload module: /tmp/tmpiatdzhbv.py
2023-01-12 17:50:11,130 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:11,132 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:11,133 - distributed.preloading - INFO - Import preload module: /tmp/tmpjgmht48i.py
2023-01-12 17:50:11,133 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-18', service_id='18')
2023-01-12 17:50:11,134 - distributed.utils - INFO - Reload module tmpxq_75d36 from .py file
2023-01-12 17:50:11,134 - distributed.preloading - INFO - Import preload module: /tmp/tmpxq_75d36.py
2023-01-12 17:50:11,134 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:11,148 - distributed.preloading - INFO - Import preload module: /tmp/tmpxii_na8e.py
2023-01-12 17:50:11,148 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-6', service_id='6')
2023-01-12 17:50:11,149 - distributed.utils - INFO - Reload module tmpf60e3pp5 from .py file
2023-01-12 17:50:11,149 - distributed.preloading - INFO - Import preload module: /tmp/tmpf60e3pp5.py
2023-01-12 17:50:11,149 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:11,153 - distributed.preloading - INFO - Import preload module: /tmp/tmp60t2lwfv.py
2023-01-12 17:50:11,153 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-14', service_id='14')
2023-01-12 17:50:11,153 - distributed.utils - INFO - Reload module tmp7rg55b3j from .py file
2023-01-12 17:50:11,154 - distributed.preloading - INFO - Import preload module: /tmp/tmp7rg55b3j.py
2023-01-12 17:50:11,154 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:11,175 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:11,181 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:11,183 - distributed.preloading - INFO - Import preload module: /tmp/tmpj6m3i3ov.py
2023-01-12 17:50:11,183 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-2', service_id='2')
2023-01-12 17:50:11,184 - distributed.utils - INFO - Reload module tmp5ecsfkid from .py file
2023-01-12 17:50:11,184 - distributed.preloading - INFO - Import preload module: /tmp/tmp5ecsfkid.py
2023-01-12 17:50:11,185 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:11,186 - distributed.preloading - INFO - Import preload module: /tmp/tmpzgtfrjqg.py
2023-01-12 17:50:11,186 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-22', service_id='22')
2023-01-12 17:50:11,186 - distributed.utils - INFO - Reload module tmpyzodyf3d from .py file
2023-01-12 17:50:11,187 - distributed.preloading - INFO - Import preload module: /tmp/tmpyzodyf3d.py
2023-01-12 17:50:11,187 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:11,197 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:11,201 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:11,209 - distributed.preloading - INFO - Import preload module: /tmp/tmpkg1evcn9.py
2023-01-12 17:50:11,209 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-9', service_id='9')
2023-01-12 17:50:11,210 - distributed.utils - INFO - Reload module tmpvfr6w3rw from .py file
2023-01-12 17:50:11,210 - distributed.preloading - INFO - Import preload module: /tmp/tmpvfr6w3rw.py
2023-01-12 17:50:11,210 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:11,218 - distributed.preloading - INFO - Import preload module: /tmp/tmpt5zrb1f7.py
2023-01-12 17:50:11,219 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-19', service_id='19')
2023-01-12 17:50:11,219 - distributed.utils - INFO - Reload module tmpl3i86okx from .py file
2023-01-12 17:50:11,220 - distributed.preloading - INFO - Import preload module: /tmp/tmpl3i86okx.py
2023-01-12 17:50:11,220 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:11,235 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:11,248 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:11,255 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:11,265 - distributed.preloading - INFO - Import preload module: /tmp/tmpdpfrnuvy.py
2023-01-12 17:50:11,265 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-16', service_id='16')
2023-01-12 17:50:11,266 - distributed.utils - INFO - Reload module tmpvlofalzh from .py file
2023-01-12 17:50:11,266 - distributed.preloading - INFO - Import preload module: /tmp/tmpvlofalzh.py
2023-01-12 17:50:11,266 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:11,267 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:11,302 - distributed.preloading - INFO - Import preload module: /tmp/tmpnknaw25k.py
2023-01-12 17:50:11,303 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-12', service_id='12')
2023-01-12 17:50:11,303 - distributed.utils - INFO - Reload module tmp3fr1rp7v from .py file
2023-01-12 17:50:11,303 - distributed.preloading - INFO - Import preload module: /tmp/tmp3fr1rp7v.py
2023-01-12 17:50:11,303 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:11,313 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:11,313 - distributed.preloading - INFO - Import preload module: /tmp/tmpc7avhpah.py
2023-01-12 17:50:11,314 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:11,343 - distributed.preloading - INFO - Import preload module: /tmp/tmpl3_x3umv.py
2023-01-12 17:50:11,343 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-17', service_id='17')
2023-01-12 17:50:11,344 - distributed.utils - INFO - Reload module tmphl3hthxj from .py file
2023-01-12 17:50:11,344 - distributed.preloading - INFO - Import preload module: /tmp/tmphl3hthxj.py
2023-01-12 17:50:11,344 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:11,348 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:11,356 - distributed.preloading - INFO - Import preload module: /tmp/tmpblrzbrp4.py
2023-01-12 17:50:11,356 - distributed.preloading - INFO - Creating preload: from libertem.common.tracing import maybe_setup_tracing; maybe_setup_tracing(service_name='default-cpu-23', service_id='23')
2023-01-12 17:50:11,357 - distributed.utils - INFO - Reload module tmpfbs5qs95 from .py file
2023-01-12 17:50:11,357 - distributed.preloading - INFO - Import preload module: /tmp/tmpfbs5qs95.py
2023-01-12 17:50:11,357 - distributed.preloading - INFO - Creating preload: libertem.preload
2023-01-12 17:50:11,357 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:11,390 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:11,402 - distributed.preloading - INFO - Import preload module: libertem.preload
2023-01-12 17:50:11,882 - distributed.worker - WARNING - Compute Failed
Key:       _do_detect-3a769958-dd25-44c4-919e-e2c5e3607b05
Function:  _do_detect
args:      ()
kwargs:    {}
Exception: 'DataSetException("OSError(\'Unable to open file (file signature not found)\')")'

[4]:

cy = 125.7
cx = 124.9
fy, fx = tuple(ds.shape.sig)
y, x = tuple(ds.shape.nav)
r = 3

Use libertem.udf.masks.ApplyMasksUDF to calculate brightfield and darkfield image for segmentation between sample and membrane.

[5]:

ring = functools.partial(
    masks.ring,
    centerX=cx,
    centerY=cy,
    imageSizeX=fx,
    imageSizeY=fy,
    radius=160,
    radius_inner=100,
)
disk = functools.partial(
    masks.circular,
    centerX=cx,
    centerY=cy,
    imageSizeX=fx,
    imageSizeY=fy,
    radius=1,
    antialiased=True
)
segmentation_udf = ApplyMasksUDF(
    mask_factories=[ring, disk],
)

[6]:

segmentation = ctx.run_udf(udf=segmentation_udf, dataset=ds, progress=True)

[7]:

fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].imshow(segmentation['intensity'].data[..., 0])
axes[1].imshow(segmentation['intensity'].data[..., 1])

[7]:

<matplotlib.image.AxesImage at 0x7f7b49ee9400>

The amorphous membrane (substrate) is masked out in subsequent processing to reduce the amount of computation and improve the clustering result.

We use agglomerative clustering with brightfield and darkfield value as feature vector. The connectivity matrix ensures that only neighboring pixels can belong to the same cluster.

[8]:

connectivity = scipy.sparse.csr_matrix(
    sklearn.feature_extraction.image.grid_to_graph(
        # Transposed!
        n_x=y,
        n_y=x,
    )
)

clusterer = sklearn.cluster.AgglomerativeClustering(
    affinity='euclidean',
    n_clusters=3,
    linkage='ward',
    connectivity=connectivity,
)

[9]:

clusterer.fit(segmentation['intensity'].data.reshape(-1, 2))
labels = clusterer.labels_.reshape((y, x))

/home/weber/miniconda3/envs/libertem39/lib/python3.9/site-packages/sklearn/cluster/_agglomerative.py:983: FutureWarning: Attribute `affinity` was deprecated in version 1.2 and will be removed in 1.4. Use `metric` instead
  warnings.warn(

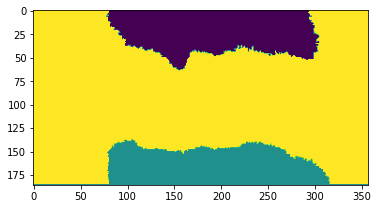
The scan dimension is clustered in three regions: Center, upper membrane and lower membrane. We identify the cluster class of the sample by evaluating the central pixel. Then we create a region of interest (ROI) of all pixels with this label.

[10]:

fig, axes = plt.subplots()
plt.imshow(labels)

[10]:

<matplotlib.image.AxesImage at 0x7f7b49e605e0>

[11]:

center_label = labels[y//2, x//2]
center_roi = labels == center_label

To highlight crystalline regions of a phase change material, use libertem.udf.crystallinity, which is integrating over the ring with rad_in and rad_out each frame spectrum which belongs to roi. The result is a measure of how present diffraction peaks besides the zero order peak are in each frame. Since the grains have random orientations, this value fluctuates strongly.

[12]:

crystal_res = run_analysis_crystall(ctx, ds, rad_in=6, rad_out=60,
                              real_center=(cy, cx), real_rad=6, roi=center_roi, progress=True)
crystal = crystal_res["intensity"].data

[13]:

plt.figure()
plt.imshow(np.log(crystal))

[13]:

<matplotlib.image.AxesImage at 0x7f7b35f3d5e0>

Sample region clustering

To generate a feature fector, we first generate a standard deviation map using libertem.udf.stddev. Then we find maxima in this standard deviation map and use the pixel value of these positions to generate a feature vector for each frame.

[14]:

stddev_res = run_stddev(ctx=ctx, dataset=ds, roi=center_roi, progress=True)

[15]:

peaks = peak_local_max(stddev_res['std'], min_distance=3, num_peaks=500)

[16]:

fig, axes = plt.subplots()
plt.imshow(stddev_res['std'])
for p in np.flip(peaks, axis=-1):
    axes.add_artist(plt.Circle(p, r, color="y", fill=False))

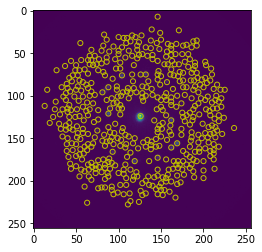
We use libertem.udf.masks.ApplyMasksUDF with a very sparse mask stack to select the pixel values for each frame. This operation is very efficient.

[17]:

masks = sparse.COO(
    shape=(len(peaks), fy, fx),
    coords=(range(len(peaks)), peaks[..., 0], peaks[..., 1]),
    data=1.
)
feature_udf = ApplyMasksUDF(
    mask_factories=lambda: masks,
    mask_dtype=bool,
    mask_count=len(peaks),
    use_sparse=True
)

[18]:

%time feature_res = ctx.run_udf(udf=feature_udf, dataset=ds, roi=center_roi, progress=True)

CPU times: user 640 ms, sys: 96.5 ms, total: 736 ms
Wall time: 2.72 s

Normalize the feature vectors to make sure that strong peaks don’t dominate the distance calculation.

[19]:

f = feature_res['intensity'].raw_data
feature_vector = f / np.abs(f).mean(axis=0)

Clustering can be done with any of clustering algorithm you like. Agglomerative clustering with a connectivity matrix for neighboring pixels lke shown here usually works well. Since the image is large in the scan dimension, the clustering can be somewhat time-consuming.

[20]:

%%time
roi_connectivity = connectivity[center_roi.flatten()][..., center_roi.flatten()]
clustering = sklearn.cluster.AgglomerativeClustering(
    metric='euclidean',
    distance_threshold=300,
    n_clusters=None,
    linkage='ward',
    connectivity=roi_connectivity
).fit(feature_vector)

labels = np.array(clustering.labels_+1)
labelmask=np.full((y, x), np.nan)
labelmask[center_roi]=labels

CPU times: user 28.8 s, sys: 639 ms, total: 29.5 s
Wall time: 29.1 s

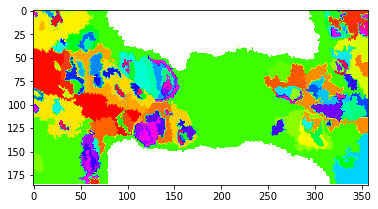
Visualize the clustering result. Note that the difference between the value assigned to each class is not a measure of similarity. A discrete color scale would be best-suited. Tab20 with 20 entries is the largest available in matplotlib and we have significantly more clusters. HSV usually achieves an acceptable differentiation of discrete values beyond 20.

[21]:

fig, axes = plt.subplots()
plt.imshow(labelmask, cmap=cm.hsv)

[21]:

<matplotlib.image.AxesImage at 0x7f7b12ea0190>

[ ]: